Ron的BLOG
0%

快速反平方根算法误差问题

Posted on

1. 问题现象

我们策划在配置技能的时候，当技能方向趋向于y轴方向的时候，发现技能方向总是有一定的偏差，进行细节调整的时候，也达不到效果，一直微调，微调到一定大小后，方向会突然偏向于另一边。如下图：

在趋向于x轴的时候，策划发现一直有4.69度想右边的偏差。进行微调也不会发生变化，直到微调到大约偏向于左边的时候，左边偏差却来到了3.79度。
也就是说有3.79+4.69=8.48度的角度，策划是指向的。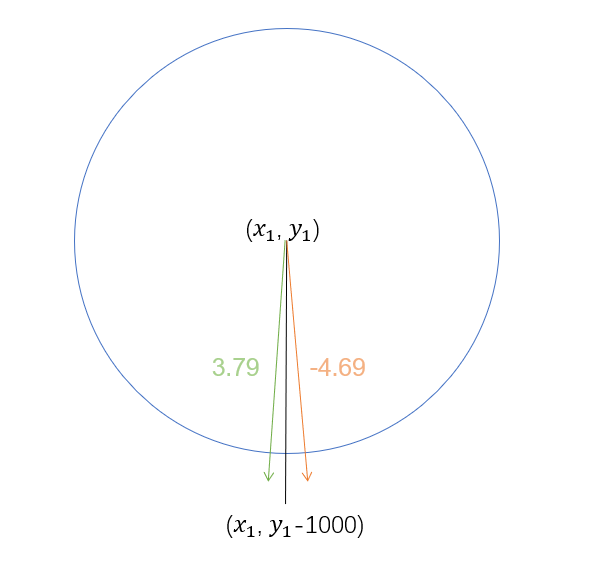
误差对比

2. 排查问题

策划配置的角度是怪物站在(x1, y1)的位置，然后怪物技能的朝向目标坐标是(x1, y1-1000)的位置。策划进行微调的时候，是对目标坐标的x轴的值进行微调，发现无法调到想要的方向。

游戏内的实现逻辑是，释放技能的时候，把怪物转到设定方向。原本怪物的方向是(0, 1)，虽然已经是策划需要的方向，但是此时也是会进行转向的运算。需要转到的目标方向也是(0, 1)。此时只要运算出怪物需要转向的角度为0即可。但事实是怪物转向逆时针转向了4.69度。

排查发现，计算转向的函数返回了这4.69度，进一步排查发现快速反平方根函数 fast_inv_sqrt 返回的值是有一定误差的。在运行 fast_inv_sqrt(1.0f) 的时候，返回的是0.998323,虽然已经很接近1了，但是仍然是有误差的。就是这小小的0.002左右的误差，最终计算角度的时候出现了4.69度的误差。
关于快速反平方根算法，我在之前的文章有解读过，可以查看 解读快速反平方根算法

3. 验证误差

下面代码是三种求反平方根的结果。调用math.h库的sqrt函数进行运算是没有误差的。
快速反平方根有牛顿迭代进行修正，一次迭代的时候，结果是0.998323，进行两次牛顿迭代的时候，数值会更加精确，来到了0.999996，小数点比一次迭代多精确3位数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
double normal_inv_sqrt(double x)
{
	return 1/sqrt(x);
}

double fast_inv_sqrt(double x)
{
	double y = x;
	double xhalf = (double)0.5 * y;
	long long i = *(long long*) (&y);
	i = 0x5fe6ec85e7de30daLL - (i >> 1);
	y = *(double*) (&i);
	y = y * ((double)1.5 - xhalf * y * y);
	// y = y * ((double)1.5 - xhalf * y * y);
	return y;
}

double fast_inv_sqrt2(double x)
{
	double y = x;
	double xhalf = (double)0.5 * y;
	long long i = *(long long*) (&y);
	i = 0x5fe6ec85e7de30daLL - (i >> 1);
	y = *(double*) (&i);
	y = y * ((double)1.5 - xhalf * y * y);
	y = y * ((double)1.5 - xhalf * y * y);
	return y;
}

int main(){
    struct vec3 a = { 0.0f, 0.0f, 1.0f };
    struct vec3 b = { 0.0f, 0.0f, 1.0f };
	printf("normal_inv_sqrt %f\n", normal_inv_sqrt(1.0f));
	printf("fast_inv_sqrt   %f\n", fast_inv_sqrt(1.0f));
	printf("fast_inv_sqrt2  %f\n", fast_inv_sqrt2(1.0f));
	return 0;
}

输出结果：

1
2
3
normal_inv_sqrt 1.000000
fast_inv_sqrt   0.998323
fast_inv_sqrt2  0.999996

4. 快速反平方根运算过程

double 类型的数据中符号位占用 1 位，指数占用 11 位，尾数占用 52 位。
那么double表示1.0f，用64位表示就是

1
2
3
4
5
6
7
8
1位符号位 11位指数    52位指数
S        E           M
0        01111111111 0000000000000000000000000000000000000000000000000000
// 双精度的公式是 F = (-1)^s * (2^(E-1023)) * (1 + 2^-52 * M)
// F= (-1)^0 * 2^(2^10-1-1023) * (1 + 2^(-52)*0)
//  = 1 * 2^0 * (1+0)
//  = 1*1*1 
//  = 1

转成long long类型，数值就是：2^62 - 2^52 = 4,607,182,418,800,017,408
转成目标值的整型：Ly=(3/2)2^52(1023-μ) - 1/2*Lx

1
2
3
4
Ly = (3/2)*2^52*(1023-μ) - 1/2*Lx
   = 6755399441055744‬ * (1023-0.04505) - 1/2*4607182418800017408
   = 6755399441055744 * 1022.95495‬ - 2303591209400008704
   = 4606878088055197846
1
2
3
4
5
6
7
8
9
1位符号位 11位指数    52位指数
S        E           M
0        01111111110 1110111010110011011001111010000011111001000000000000
// S = 0
// E = 2^10 - 1 - 1 = 1022
// M = 4199268882550784
// F = (-1)^s * (2^(E-1023)) * (1 + 2^-52 * M)
//   = 1 * 2^(1022-1023) * (1+2^-52 * 4199268882550784)
//   = 0.96621249999998

结果0.966是尚未进行牛顿迭代的结果，误差要大的多，进行一次迭代之后，数值是0.998323，进行两次迭代之后是0.999996。

5. 角度误差对比

虽然快速快速反平方根运算计算1的时候，误差在0.002，看起来也不是很大。但是在运算角度的时候，会放大这个误差，误差。特别是在角度-10度到10度，170度到190度之间。

误差对比

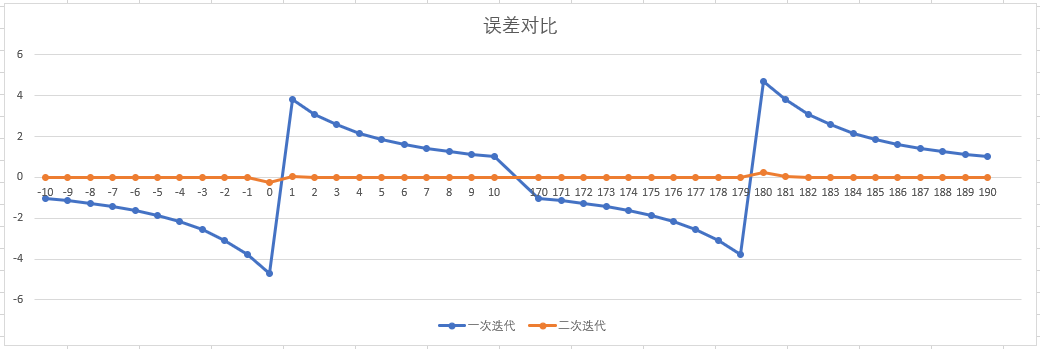
一次迭代 vs 两次迭代 的误差

转向角度 一次迭代 二次迭代
-10 -1.03602 -0.00275
-9 -1.14083 -0.00306
-8 -1.26681 -0.00341
-7 -1.42067 -0.00392
-6 -1.61165 -0.00464
-5 -1.85288 -0.00556
-4 -2.16291 -0.00695
-3 -2.56751 -0.00925
-2 -3.09991 -0.01385
-1 -3.79752 -0.02741
0 -4.69231 -0.23573
1 3.797516 0.027412
2 3.099911 0.013848
3 2.567509 0.009251
4 2.162912 0.006946
5 1.852875 0.005561
6 1.611654 0.004638
7 1.420678 0.003922
8 1.26681 0.003411
9 1.140832 0.003056
10 1.036024 0.002753
170 -1.03599 -0.00273
171 -1.14081 -0.00303
172 -1.26684 -0.00344
173 -1.42067 -0.00392
174 -1.61162 -0.00462
175 -1.85288 -0.00556
176 -2.16292 -0.00694
177 -2.56751 -0.00925
178 -3.09991 -0.01384
179 -3.79752 -0.02742
180 4.692313 0.235737
181 3.797517 0.027416
182 3.099909 0.013838
183 2.567509 0.009248
184 2.16293 0.006953
185 1.852853 0.005532
186 1.611652 0.004645
187 1.420666 0.003921
188 1.266836 0.003442
189 1.140806 0.003033
190 1.03603 0.002759
  • 一次迭代里面，误差超过1度的在-10到10度，170到190度之间。
  • 在0度和180度达到了最大误差值，分别是-4.69度和4.69度。
  • 在0度到1度偏转的差值，来到了-4.69-3.79=-8.48度，将近10度了，也就是说有这10度，策划怎么调都调不到这个方向的。
  • 两次迭代之后，数据要好得多，最大误差只有0.23度，这个数值玩家已经很难观察到了。

6. 修复方法

修复问题有三种：

  • 第一种：在角度趋向于x轴，y轴的四个方向的时候，写死结果；
  • 第二种：把快速反平方根函数修改为 1/sqrt(x)，这样结果是没有误差的；
  • 第三种：在快速反平方根中，把结果进行两次牛顿迭代，提高精度。

第一种可以解决部分情况，但是如果策划需要有偏差的时候，会把结果修改为没有偏差，会引入新的问题。第二种结果是最好的，但是不知道sqrt函数的内容，无法预估带来的内存影响，而且快速反平方根函数已经运行了多年。最后选了第三种，提高的精度已经完全足够使用了。