Ron的BLOG

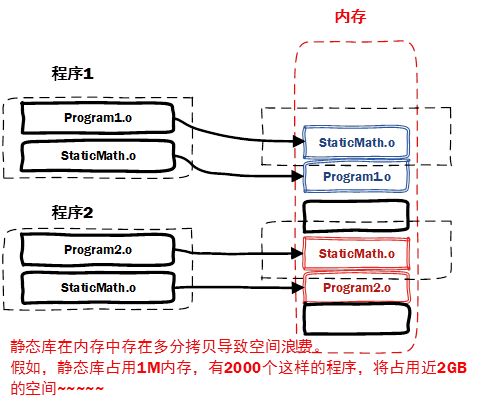
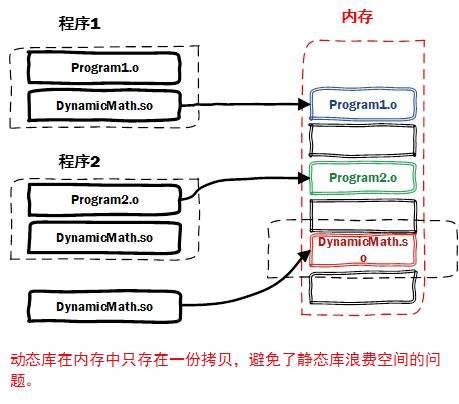
MongoDB 有一个叫覆盖索引的feature

意思是查询数据的时候，过滤条件和查询字段刚好都是索引，那么MongoDB可能会选择从索引表查询结果，而不需要查询Document。

为什么说是可能的，而不是必须的，这取决于MongoDB的查询计划。

出现问题

最近收到运维的反馈，说某个版本之后开服时间大幅度变长了。这个版本确实是新增了一个数据库表，是从另一个表拆分出来的数据，且在开服的时候需要全表扫描。两个表加起来的数据量在更新前后是一致的。所以预期上不应该出现开服时间大幅度变长的情况。

首先检查了两张表的差别，原来需要扫描的表是有索引字段的，且查询的结果刚好也是索引字段。而新增的是没有索引的。所以怀疑有索引的表，会触发MongoDB的覆盖索引查询，而没有增加的，只能全表扫描。通过对新表增加索引进行对比，发现没有显著的变化。

覆盖索引查询

首先先定位一下，覆盖索引查询 到底有没有被执行。执行db.setProfilingLevel(2); 打开MongoDB的查询分析功能。

1
2
3
4
5

use [db];
db.setProfilingLevel(2);
# 参数 0 是关闭
# 参数 1 是记录慢查询
# 参数 2 是记录所有操作

然后等Skynet这边执行查询操作，查询后在mongo里面执行 db.system.profile.find({"ns" : "[db].[collection]"}).sort({ ts: -1 }).limit(10) 查询某个集合的查询结果。

1
2
3
4
5

use [db];
# 查看结果
db.system.profile.find().sort( { ts : -1 } )
# 查看针对某个表的查询结果
db.system.profile.find({"ns" : "[db].[collection]"}).sort({ ts: -1 }).limit(10);

在结果里面查看execStats.inputStage.stage 的结果就可以定位是否使用了覆盖索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

{
   "op":"query",
   "execStats":{
      "memLimit":104857600,
      "type":"simple",
      "totalDataSizeSorted":0,
      "usedDisk":false,
      "inputStage":{
         "stage":"COLLSCAN",
         "nReturned":0,
         "executionTimeMillisEstimate":0,
         "works":2,
         "advanced":0,
         "needTime":1,
         "needYield":0,
         "saveState":0,
         "restoreState":0,
         "isEOF":1,
         "direction":"forward",
         "docsExamined":0
      }
   }
}

解决办法

出现这样的问题，是因为在查询数据的时候，过滤条件为空的时候，MongoDB会优先进行全表扫描。当过滤条件不为空，且条件字段刚好是索引的时候，基本上都能触发覆盖索引查询。

针对这种情况，可以使用hint函数，告诉MongoDB，强制使用覆盖索引查询的方式，不在需要进行MongoDB的查询决策了。

下面是未指定hint的查询情况，可以看到 executionStats.executionStages.inputStage.stage的结果是COLLSCAN。未使用覆盖索引查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

> db.role.find({},{uid:1,'_id':0}).explain("executionStats")
{
        "queryPlanner" : {
                ...
        },
        "executionStats" : {
                "executionSuccess" : true,
                "nReturned" : 7,
                "executionTimeMillis" : 0,
                "totalKeysExamined" : 0,
                "totalDocsExamined" : 7,
                "executionStages" : {
                        "inputStage" : {
                                "stage" : "COLLSCAN",
                                "nReturned" : 7,
                                "executionTimeMillisEstimate" : 0,
                                "works" : 9,
                                "advanced" : 7,
                                "needTime" : 1,
                                "needYield" : 0,
                                "saveState" : 0,
                                "restoreState" : 0,
                                "isEOF" : 1,
                                "direction" : "forward",
                                "docsExamined" : 7
                        }
                }
        }
}

下面是使用hint的情况，可以看到 executionStats.executionStages.inputStage.stage的结果是IXSCAN。未使用覆盖索引查询。查看 totalKeysExamined =7，totalDocsExamined = 0，也可以知道查询的7天数据全部来源于索引表，并未从文档查询过数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

> db.role.find({},{uid:1,'_id':0}).hint({uid:1}).explain("executionStats")
{
        "queryPlanner" : {
                ...
        },
        "executionStats" : {
                "executionSuccess" : true,
                "nReturned" : 7,
                "executionTimeMillis" : 0,
                "totalKeysExamined" : 7,
                "totalDocsExamined" : 0,
                "executionStages" : {
                        "stage" : "PROJECTION_COVERED",
                        "inputStage" : {
                                "stage" : "IXSCAN",
                                "nReturned" : 7,
                                "executionTimeMillisEstimate" : 0,
                                "works" : 8,
                                "advanced" : 7,
                                "needTime" : 0,
                                "needYield" : 0,
                                "saveState" : 0,
                                "restoreState" : 0,
                                "isEOF" : 1,
                                "keyPattern" : {
                                        "uid" : 1
                                },
                                "indexName" : "uid_1",
                                "isMultiKey" : false,
                                "multiKeyPaths" : {
                                        "uid" : [ ]
                                },
                                "isUnique" : true,
                                "isSparse" : false,
                                "isPartial" : false,
                                "indexVersion" : 2,
                                "direction" : "forward",
                                "indexBounds" : {
                                        "uid" : [
                                                "[MinKey, MaxKey]"
                                        ]
                                },
                                "keysExamined" : 7,
                                "seeks" : 1,
                                "dupsTested" : 0,
                                "dupsDropped" : 0
                        }
                }
        }
}

最后

针对一些要查询全表某些字段，而这些字段又刚好是索引的情况。可以使用hint来主动告诉MongoDB使用覆盖索引查询结果。另外因为MongoDB查询数据默认是会返回_id字段的，这个字段也会影响到是否触发覆盖索引查询的情况，可能会即使用了索引查询，也会查询文档的情况。所以如果这个字段不需要使用，是需要去除的。

skynet比较旧的版本是不支持hint操作的。这个需要修改skynet源码或者升级skynet版本来支持。因为后面的版本skynet使用的是op_msg协议接入MongoDB了。而我们MongoDB版本还不支持，所以只能修改skynet源码才能实现。

之前写了一个纯lua实现的模块 纯lua实现统计函数运行时间和调用次数。但是统计的hook函数本身就太耗时了，简单使用还行，如果想要在本身就对性能比较敏感的地方使用，就完全不可行了。所以写了一版纯c语言的版本。

实现的完整代码在：https://github.com/rondsny/lua-profile/blob/main/lua-profiler.c

设置hook

原理是一样的，只是换了c实现而已。lua的c api提供了lua_sethook函数。

void lua_sethook (lua_State *L, lua_Hook f, int mask, int count);
设置一个调试用钩子函数。

参数 f 是钩子函数。 mask 指定在哪些事件时会调用： 它由下列一组位常量构成 LUA_MASKCALL， LUA_MASKRET， LUA_MASKLINE， LUA_MASKCOUNT。 参数 count 只在掩码中包含有 LUA_MASKCOUNT 才有意义。 对于每个事件，钩子被调用的情况解释如下：

call hook: 在解释器调用一个函数时被调用。 钩子将于 Lua 进入一个新函数后， 函数获取参数前被调用。
return hook: 在解释器从一个函数中返回时调用。 钩子将于 Lua 离开函数之前的那一刻被调用。 没有标准方法来访问被函数返回的那些值。
line hook: 在解释器准备开始执行新的一行代码时， 或是跳转到这行代码中时（即使在同一行内跳转）被调用。 （这个事件仅仅在 Lua 执行一个 Lua 函数时发生。）
count hook: 在解释器每执行 count 条指令后被调用。 （这个事件仅仅在 Lua 执行一个 Lua 函数时发生。）

我们同样监听LUA_HOOKCALL和LUA_HOOKRET这两种事件。对应的是一个函数被调用和返回时候的hook。对于尾调用其实意义不是很大，我们从上一层统计也能包含，只是统计的位置会不一样，所以这里不对尾调用的情况额外区分统计。

在调用lua_sethook的时候，我们第三个参数传入LUA_MASKCALL和LUA_MASKRET。

1

lua_sethook(L, profiler_hook, LUA_MASKCALL | LUA_MASKRET, 0);

统计

统计上也是类似的，只不过c这边需要一个map结构，本来是想起一个lua_State，然后用来记录统计数据，因为lua的table结构本身就是一个非常好的map结构。后来考虑尽量减少性能损耗，就额外实现了哈希表结构。这里其实只是需要一个哈希表而已，实现只要没问题都可以。

首先是监听到call的时候，创建一个item用于记录调用时间和函数信息，然后塞入到一个后入先出的数组结构中。

当发生return的时候，我们就从数组中拿出最后一个item，这个item必然是当前return的call（此处把尾调用的return记录到最开始的call里面）。此时进行时间差统计，并且去除调用函数的时间，则是当前函数的执行时间。然后统计到哈希表中。如果没有则创建记录，有则把执行时间和调用次数统计上去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

static void profiler_hook(lua_State *L, lua_Debug *arv) {
    lua_Debug ar;
    lua_getstack(L, 0, &ar);
    lua_getinfo(L, "nSlf", &ar);

    if (arv->event == LUA_HOOKCALL) {
        const void* point = lua_topointer(L, -1);
        uint64_t now = get_high_precision_time();
        struct call_item* item = (struct call_item*)malloc(sizeof(struct call_item));
        item->point = point;
        item->name = ar.name ? ar.name : "?";
        item->source = ar.source ? ar.source : "?";
        item->line = ar.currentline;
        item->call_time = now;
        item->sub_cost = 0;
        push_call_item(item);
    }
    else if (arv->event == LUA_HOOKRET) {
        struct call_item* item = pop_call_item();
        if (item == NULL) {
            return;
        }
        uint64_t now = get_high_precision_time();
        uint64_t cost = now - item->call_time;
        uint64_t key = (uint64_t)((uintptr_t)item->point);
        profile_record* record = (profile_record*)game_hashtbl_get(hashtbl, key);
        if(record==NULL){
            record = (profile_record*)malloc(sizeof(profile_record));
            record->call_count = 1;
            record->total_time = cost - item->sub_cost;
            record->line = item->line;
            strncpy(record->name, item->name, sizeof(record->name));
            strncpy(record->source, item->source, sizeof(record->source));
            game_hashtbl_insert(hashtbl, key, record);
        }else{
            record->call_count++;
            record->total_time += cost - item->sub_cost;
        }
        if(CALL_STACK->head){
            CALL_STACK->head->sub_cost += cost;
        }
        free(item);
    }
}

性能提升

纯lua版本数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

use profiler_pure_lua
======== profiler start ========
total time is   22.453125
========================================
        time, percent,   count, function
----------------------------------------
52.5470021956,  99.52%, 8160000, deep2                         : test_profiler.lua:1
0.2536309999,   0.48%,     200, call_func                     : test_profiler.lua:14
0.0007711950,   0.00%,       2, loop                          : test_profiler.lua:23
0.0006873300,   0.00%,      10, nono                          : test_profiler.lua:49
0.0004256395,   0.00%,       5, clock                         : [C]:-1
0.0001266750,   0.00%,       1, foo                           : test_profiler.lua:35
0.0000041250,   0.00%,       1, foo2                          : test_profiler.lua:31
0.0000000000,   0.00%,       1, stop                          : ./profiler_pure_lua.lua:80
======== profiler end total_time ==========     52.802648159995

c语言版本数据：

1
2
3
4
5
6
7
8
9
10
11
12

use c unction
total time is   2.0
0.000321 (0.01%)           1                 print  =[C]:-1
0.000169 (0.00%)           2                     ?  =[C]:-1
0.000011 (0.00%)           1                 clock  =[C]:-1
0.000021 (0.00%)          10                  nono  @test_profiler.lua:50
0.000010 (0.00%)           1                   foo  @test_profiler.lua:36
0.000000 (0.00%)           1                  foo2  @test_profiler.lua:32
0.000167 (0.00%)           2                  loop  @test_profiler.lua:24
0.035776 (0.68%)         200             call_func  @test_profiler.lua:15
5.232884 (99.31%)     8160000                 deep2  @test_profiler.lua:2
total time is   5.269360

以上例子可以看到，c语言版本运行统计耗时是5.26秒，纯lua的耗时是52.8秒。而实际的运行时间，没有hook的耗时是0.59秒。c语言版本是2秒，纯lua的耗时是22.45秒。

从数据上看，我们并不允许线上产生22秒的卡顿，但是极端情况下，卡2秒可能还是可以接收的。改成c语言实现后，甚至可以在线上使用。

lua没有专门查看cpu占用的工具，只能自己撸一个。得益于lua提供了debug.sethook函数，可以在函数调用和返回的时候调用一个设置好的hook函数。在hook函数可以进行数据的统计。
实现起来也极其简单，在函数调用的时候记录调用时间，在函数返回的时候进行时间差统计，这样就得到了一个函数的运行时间。

简单统计

原理是基于debug.sethook，下面写逻辑统计时间就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

local function cc(i)
    if i <= 0 then
        return 0
    end
    cc(i-1)
end

local function aa()
    local j = 0
    for i=1, 100 do
        cc(10)
    end
end

local lst_item = {}
local map_record = {}
debug.sethook(function(hook_type)
        local func_info = debug.getinfo(2, 'nSl')
        local key = func_info.short_src ..":".. func_info.linedefined

        local now = os.clock()
        if hook_type == "call" then
            table.insert(lst_item,{
                call_time = now,
                key = key,
            })
        elseif hook_type == "return" then
            local item = table.remove(lst_item)
            if not item then return end

            local record = map_record[key]
            if record then
                record.call_count = record.call_count + 1
                record.total_time = record.total_time + (now - item.call_time)
            else
                map_record[key] = {
                    call_count = 1,
                    total_time = now - item.call_time,
                    name = func_info.name,
                    line = func_info.linedefined,
                    source = func_info.short_src,
                }
            end
        end
    end, 'cr', 0)

local start_time = os.clock()
aa()

local total_time = 0
for k,v in pairs(map_record) do
    total_time = total_time + v.total_time
    local use_time = string.format("%4.3f", v.total_time)
    print(string.format("%7s  %10d  %20s  %s", use_time, v.call_count, v.name, k))
end
print("-----------------------")
print("total_time: ", total_time)
print("real use time:", os.clock() - start_time)

output:

1
2
3
4
5

  0.016           1                    aa  test.lua:8
  0.062        1100                    cc  test.lua:1
-----------------------
total_time:     0.078125
real use time:  0.015625

总耗时0.15625秒，但是统计的函数总时间却是0.078125秒，与实际不相符。

递归重复统计

从上面的例子可以发现，只记录call和return进行插值统计时，当出现递归函数的时候，数据是有问题的，递归函数的时间会重叠，就会出现多余的情况。并且os.clock()函数的精度已经不够了，对于简单的函数内容，os.clock计算出来的差值是0，这样统计出来的结果也是有问题的。下面增加去除子函数运行的时间，并且把获取时间的函数替换成高精度时间函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

local lst_item = {}
local map_record = {}
debug.sethook(function(hook_type)
        local func_info = debug.getinfo(2, 'nSl')
        local key = func_info.short_src ..":".. func_info.linedefined

        local now = gettime()
        if hook_type == "call" then
            table.insert(lst_item,{
                call_time = now,
                key = key,
                sub_cost = 0,
                name = func_info.name,
            })
        elseif hook_type == "return" then
            local item = table.remove(lst_item)
            if not item then return end

            local record = map_record[key]
            if record then
                record.call_count = record.call_count + 1
                record.total_time = record.total_time + (now - item.call_time - item.sub_cost)
            else
                map_record[key] = {
                    call_count = 1,
                    total_time = now - item.call_time - item.sub_cost,
                    name = item.name,
                    line = func_info.linedefined,
                    source = func_info.short_src,
                }
            end
            if #lst_item > 0 then
                lst_item[#lst_item].sub_cost = lst_item[#lst_item].sub_cost + (now - item.call_time)
            end
        end
    end, 'cr', 0)

output:

1
2
3
4
5

  0.0001655           1                    aa  test.lua:12
  0.0034916        1100                    cc  test.lua:5
-----------------------
total_time:     0.0039355754852295
real use time:  0.0062041282653809

尾递归问题

下面把cc函数改成尾递归，执行结果如下：

1
2
3
4
5
6

  0.0000079           5               gettime  [C]:-1
  0.0018032         100                    cc  test.lua:5
  0.0002387           1                    aa  test.lua:12
-----------------------
total_time:     0.0020496845245361
real use time:  0.0020508766174316

这里发现cc函数的调用次数统计也有1100次变成了100次。如果需要把尾递归调用也统计进去，那就需要监听hook_type为tail call类型的情况。因为尾递归只有一次return，所以需要在return的时候进行额外的处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

local lst_item = {}
local map_record = {}
debug.sethook(function(hook_type)
        local func_info = debug.getinfo(2, 'nSl')
        local key = func_info.short_src ..":".. func_info.linedefined

        local now = gettime()
        if hook_type == "call" or hook_type == 'tail call' then
            table.insert(lst_item,{
                call_time = now,
                key = key,
                sub_cost = 0,
                name = func_info.name,
                is_tail = hook_type == 'tail call',
            })
        elseif hook_type == "return" then
            local is_tail = true
            while is_tail and #lst_item > 0 do
                local item = table.remove(lst_item)

                is_tail = item.is_tail
                local record = map_record[key]
                if record then
                    record.call_count = record.call_count + 1
                    record.total_time = record.total_time + (now - item.call_time - item.sub_cost)
                else
                    map_record[key] = {
                        call_count = 1,
                        total_time = now - item.call_time - item.sub_cost,
                        name = item.name,
                        line = func_info.linedefined,
                        source = func_info.short_src,
                    }
                end
                if #lst_item > 0 then
                    lst_item[#lst_item].sub_cost = lst_item[#lst_item].sub_cost + (now - item.call_time)
                end
            end
        end
    end, 'cr', 0)

output:

1
2
3
4
5
6

  0.0018744        1100                   nil  test.lua:5
  0.0004456           1                    aa  test.lua:12
  0.0010464          15               gettime  [C]:-1
-----------------------
total_time:     0.0033664703369141
real use time:  0.0023291110992432

这里发现cc的函数名是没有成功获取到的，这是因为尾递归的缘故。其实这里也不一定要改成要统计尾递归函数，真实的lua堆栈也没有新的函数堆栈的，所以获取如上不分尾递归统计的结果更符合实际。

缺点

由于是使用了hook，这也是运行一次函数就会调用两次hook函数，这意味着带来了额外的开销，对实际统计函数的运行时间带来了额外的影响，数据也不准确。这里可以改成c语言来实现统计效果，性能会提升非常多，甚至可以在生产环境轻度使用。

以上实现完整代码在：https://github.com/rondsny/lua-profile

我们游戏已经上线五年了，线上在线并没有那么高了，但是占用的内存还是很高。对于一个老游戏来说，优化内存带来的性价比其实并不高，对kpi表现也没有太多收益。但是我们搞技术的，骨子里就是会被有难度有挑战的事情吸引。那就干吧！

我们是基于Skynet框架的游戏服务器，一个玩家一个Skynet服务（以下简称服务），一个场景分线一个服务，一个战斗副本一个服务。除此之外还有各种业务模块的服务。使用Skynet的GM Console命令，可以收集每个服务占用的lua内存和c内存。由于c内存集中在sharedata上面，这里就不展开说了，只针对lua内存来展开。进行统计发现玩家服务占总内存的46%，场景占20%，战斗副本占30%。

第一步，优化了玩家服务池的数量。当初为了让开新服的时候更加顺滑，有个玩家服务池的功能，在开服会创建一定量的玩家服务。这样玩家登录的时候不再需要创建服务，只需要从玩家服务池申请一个，再初始化数据就可以了。但是对于已经上线5年的项目来说，已经没有这种开服压力了，甚至已经填充不满池子了。这里的优化很简单，降低池子大小就可以了。

第二步，优化掉了orm的一些元表。我们还实现了一个工具，通过遍历和汇总lua的内存数据，并进行树状绘图，用来快速观察内存占用。通过分析，我们发现有很多相同的占用312个字节的元表出现。我们找到这个元表添加的代码，发现orm针对每个list和map类型的数据都会创建一个元表，这个元表包含了5个键值对。因为我们玩家数据量非常大，list类型和map类型的数据非常之多。譬如背包，卡牌，属性这些。找到问题了，优化其实也是比较简单的，元表是需要的，但是不需要每个orm对象都创建一个新的元表，所有的list类型都可以挂同一个元表，map也是。两个table就可以了，然后每个对象只有一个引用的内存占用。

第三步，优化掉了我们卡牌的历史属性。这里是业务问题，我们卡牌强化是会掉级的，所以玩法上记录了每一个强化等级的属性，以方便掉级的时候需要用。这里的属性内容比较多，等级也有15级，所以存储的内容就比较多了。但是这个属性在战斗的时候其实是不生效的。由于属性太多，如果一开始业务针对那些不会掉级的等级不保留属性并且进行保底机制处理的话，也会节省不少内存。考虑到这些数据已经挂在玩家身上了，目前也没有保底的机制。优化上，我们增加了一个缓存层，把玩家的这些历史属性进行存库处理，玩家使用的时候再加载到缓存中。
我们也把这个功能做成了通用化，别的系统也可以使用，只要业务上数据量大，查询少。缓存我们使用了最近最少使用lru算法，玩家不用的时候，到了过期时间就会删除缓存和存储。

第四步，优化掉了过期商店商品。还是因为是五年的项目了，我们运营加了非常多的商店和商品配置。并且有非常多有时效性的商品，并且早就过期了。但是这些配置仍然存在（因为我们要求不能删除配置表），玩家身上也有存储。运营上来说，我们是不会再重新开卖这些商品（可以理解为货架），就算是重新卖道具，也是会新建一个货架来卖。既然也用不上，就没有必要继续占用内存了，就把过期半年以上的商品删掉。

第五步，修改了patch代码的加载时机。原本是只要创建玩家服务，patch代码就会加载到内存。而且patch代码一般都有一些很大的表，例如玩家id，商品id，道具id这些，所以加载到内存还是不小的。patch的逻辑是每个patch每个玩家只需要执行一次。这里优化是改成要执行patch的时候才require patch文件。

第六步，优化了战斗属性字段数量。我们游戏的属性非常多，有七百多个。有好几处遍历属性配置表生成初始属性的逻辑，但是并不是每个战斗对象都会使用到每一个属性。而且真实生效的战斗属性也没那么多，很多属性都是当成状态使用的。这里优化改成有具体属性值的时候，才生成属性字段。没有的都访问一个共用的默认值（一个服务只需要一个）。这个优化是非常明显的，毕竟游戏越火，玩家越多，战斗对象越多。

手段上主要是要排查内存占用到了那里，大头是谁。lua因为存在循环引用的问题，非常不好统计。我们是通过先遍历虚拟机，然后记录对象的内存，以及父节点。之后对这些存在循环引用的数据生成一个树状结构。这一步还是比较麻烦的，首先父节点存在多个，需要选一个比较合适的，然后还要断开循环引用。这一步处理的不好生成的树就会长得不好。长得不好的树非常影响我们查看内存占用的业务结构。选父节点上，尽量选择地址小，而且是table类型的父节点。断开循环引用，如果是纯环结构，那断开地址最大对象的父节点关系。这样操作后，得到的树状结构基本上比较符合业务逻辑。

通过以上一套组合拳，我们玩家服务的内存降低了50%。场景服务内存降低了70%，战斗副本服务降低了40%。整个skynet进程，lua占用内存降低了70%，效果非常明显。

1. 问题现象

我们策划在配置技能的时候，当技能方向趋向于y轴方向的时候，发现技能方向总是有一定的偏差，进行细节调整的时候，也达不到效果，一直微调，微调到一定大小后，方向会突然偏向于另一边。如下图：

在趋向于x轴的时候，策划发现一直有4.69度想右边的偏差。进行微调也不会发生变化，直到微调到大约偏向于左边的时候，左边偏差却来到了3.79度。
也就是说有3.79+4.69=8.48度的角度，策划是指向的。

2. 排查问题

策划配置的角度是怪物站在(x1, y1)的位置，然后怪物技能的朝向目标坐标是(x1, y1-1000)的位置。策划进行微调的时候，是对目标坐标的x轴的值进行微调，发现无法调到想要的方向。

游戏内的实现逻辑是，释放技能的时候，把怪物转到设定方向。原本怪物的方向是(0, 1)，虽然已经是策划需要的方向，但是此时也是会进行转向的运算。需要转到的目标方向也是(0, 1)。此时只要运算出怪物需要转向的角度为0即可。但事实是怪物转向逆时针转向了4.69度。

排查发现，计算转向的函数返回了这4.69度，进一步排查发现快速反平方根函数 fast_inv_sqrt 返回的值是有一定误差的。在运行 fast_inv_sqrt(1.0f) 的时候，返回的是0.998323,虽然已经很接近1了，但是仍然是有误差的。就是这小小的0.002左右的误差，最终计算角度的时候出现了4.69度的误差。
关于快速反平方根算法，我在之前的文章有解读过，可以查看 解读快速反平方根算法

3. 验证误差

下面代码是三种求反平方根的结果。调用math.h库的sqrt函数进行运算是没有误差的。
快速反平方根有牛顿迭代进行修正，一次迭代的时候，结果是0.998323，进行两次牛顿迭代的时候，数值会更加精确，来到了0.999996，小数点比一次迭代多精确3位数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

double normal_inv_sqrt(double x)
{
	return 1/sqrt(x);
}

double fast_inv_sqrt(double x)
{
	double y = x;
	double xhalf = (double)0.5 * y;
	long long i = *(long long*) (&y);
	i = 0x5fe6ec85e7de30daLL - (i >> 1);
	y = *(double*) (&i);
	y = y * ((double)1.5 - xhalf * y * y);
	// y = y * ((double)1.5 - xhalf * y * y);
	return y;
}

double fast_inv_sqrt2(double x)
{
	double y = x;
	double xhalf = (double)0.5 * y;
	long long i = *(long long*) (&y);
	i = 0x5fe6ec85e7de30daLL - (i >> 1);
	y = *(double*) (&i);
	y = y * ((double)1.5 - xhalf * y * y);
	y = y * ((double)1.5 - xhalf * y * y);
	return y;
}

int main(){
    struct vec3 a = { 0.0f, 0.0f, 1.0f };
    struct vec3 b = { 0.0f, 0.0f, 1.0f };
	printf("normal_inv_sqrt %f\n", normal_inv_sqrt(1.0f));
	printf("fast_inv_sqrt   %f\n", fast_inv_sqrt(1.0f));
	printf("fast_inv_sqrt2  %f\n", fast_inv_sqrt2(1.0f));
	return 0;
}

输出结果：

1
2
3

normal_inv_sqrt 1.000000
fast_inv_sqrt   0.998323
fast_inv_sqrt2  0.999996

4. 快速反平方根运算过程

double 类型的数据中符号位占用 1 位，指数占用 11 位，尾数占用 52 位。
那么double表示1.0f，用64位表示就是

1
2
3
4
5
6
7
8

1位符号位 11位指数    52位指数
S        E           M
0        01111111111 0000000000000000000000000000000000000000000000000000
// 双精度的公式是 F = (-1)^s * (2^(E-1023)) * (1 + 2^-52 * M)
// F= (-1)^0 * 2^(2^10-1-1023) * (1 + 2^(-52)*0)
//  = 1 * 2^0 * (1+0)
//  = 1*1*1 
//  = 1

转成long long类型，数值就是：2^62 - 2^52 = 4,607,182,418,800,017,408
转成目标值的整型：Ly=(3/2)2^52(1023-μ) - 1/2*Lx

1
2
3
4

Ly = (3/2)*2^52*(1023-μ) - 1/2*Lx
   = 6755399441055744‬ * (1023-0.04505) - 1/2*4607182418800017408
   = 6755399441055744 * 1022.95495‬ - 2303591209400008704
   = 4606878088055197846

1
2
3
4
5
6
7
8
9

1位符号位 11位指数    52位指数
S        E           M
0        01111111110 1110111010110011011001111010000011111001000000000000
// S = 0
// E = 2^10 - 1 - 1 = 1022
// M = 4199268882550784
// F = (-1)^s * (2^(E-1023)) * (1 + 2^-52 * M)
//   = 1 * 2^(1022-1023) * (1+2^-52 * 4199268882550784)
//   = 0.96621249999998

结果0.966是尚未进行牛顿迭代的结果，误差要大的多，进行一次迭代之后，数值是0.998323，进行两次迭代之后是0.999996。

5. 角度误差对比

虽然快速快速反平方根运算计算1的时候，误差在0.002，看起来也不是很大。但是在运算角度的时候，会放大这个误差，误差。特别是在角度-10度到10度，170度到190度之间。

一次迭代 vs 两次迭代 的误差

• 一次迭代里面，误差超过1度的在-10到10度，170到190度之间。
• 在0度和180度达到了最大误差值，分别是-4.69度和4.69度。
• 在0度到1度偏转的差值，来到了-4.69-3.79=-8.48度，将近10度了，也就是说有这10度，策划怎么调都调不到这个方向的。
• 两次迭代之后，数据要好得多，最大误差只有0.23度，这个数值玩家已经很难观察到了。

6. 修复方法

修复问题有三种：

• 第一种：在角度趋向于x轴，y轴的四个方向的时候，写死结果；
• 第二种：把快速反平方根函数修改为 1/sqrt(x)，这样结果是没有误差的；
• 第三种：在快速反平方根中，把结果进行两次牛顿迭代，提高精度。

第一种可以解决部分情况，但是如果策划需要有偏差的时候，会把结果修改为没有偏差，会引入新的问题。第二种结果是最好的，但是不知道sqrt函数的内容，无法预估带来的内存影响，而且快速反平方根函数已经运行了多年。最后选了第三种，提高的精度已经完全足够使用了。

判断一个点是否在三角形内，可以简化为一个点与三角形三条边的关系，所以涉及到两个知识点：

• 线的表达
• 点与线的关系

1. 线的表达式

线一般由两个点表示，如A点 $(x_1, y_1)$ 到B点 $(x_2, y_2)$ 的线。线的方程是：

转换一下

其中 $(y_2 - y_1)$ ，$(x_1 - x_2)$ 和 $x_2y_1 - x_1y_2$ 都是确定值，那么一个A点到B点的线可以转换成下面表达式：

使用a,b,c三个常数可以表示一条直线。
注意：以上表达式的线都是带方向的线。

2. 点与线的关系

点与线的关系有三种，点在线的左边，右边或点在线上。
线有上面的表达式之后，这个关系就比较简单表达了：

以上表达式的结果有三种：

• 小于0，表示点在线的左边；
• 大于0，表示点在线的右边；
• 等于0，表示点在线上。

3. 点在三角形内

当一个点在三角形的三条边的同一侧的时候，点就在三角形内。
那么只要点与线的关系一致，则点在三角形内。

以上三点的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

typedef struct line
{
    float a;
    float b;
    float c;
} Line;


// 线的表达式
void pointToLine(float x1, float y1, float x2, float y2, Line *l){
    l->a = y2 - y1;
    l->b = x1 - x2;
    l->c = x2*y1 - x1*y2;
}

// 点与线的关系
float pointLineRelation(float x, float y, Line *l){
    return l->a * x + l->b * y + l->c;
}

// 点是否在三角形内
int isPointInTriangle(float x, float y,
    float x1, float y1,
    float x2, float y2,
    float x3, float y3
){
    Line line_obj1, line_obj2, line_obj3;

    Line *line1 = &line_obj1;
    Line *line2 = &line_obj2;
    Line *line3 = &line_obj3;

    pointToLine(x1, y1, x2, y2, line1);
    pointToLine(x2, y2, x3, y3, line2);
    pointToLine(x3, y3, x1, y1, line3);

    float r1 = pointLineRelation(x, y, line1);
    float r2 = pointLineRelation(x, y, line2);
    float r3 = pointLineRelation(x, y, line3);

    if(r1*r2<0){
        return 0;
    }

    if(r1*r3<0){
        return 0;
    }

    return 1;
}

-1. 涉及知识

1. float单精度的内存表示方式；
2. 对数和指数；
3. 牛顿方法/牛顿迭代。

0. 背景

在标准化向量计算的时候，会频繁使用。譬如计算A点到B点的方向，需要计算标准化向量。

1
2
3
4

float len = sqrt(x^2 + y^2 + z^2);
float x_nor = x/len;
float y_nor = y/len;
float z_nor = z/len;

1. 计算下真实的 $1/\sqrt{5}$ = ？答案为：0.44721359

2. 代码计算过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

// 快速反平方根
float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y = number;
    printf("number为 = %f\n", y);
    i = * ( long * ) &y;         // evil floating point bit hack
    printf("转换为long = %d\n", i);
    i = 0x5f3759df - ( i >> 1 ); // what the fuck?
    printf("long的结果 = %d\n", i);
    y = * ( float * ) &i;
    printf("转换为float = %f\n", y);
    y = y * ( threehalfs - ( x2 * y * y ));  // 1st iteration
    printf("Netown 迭代1次 = %f\n", y);
    y = y * ( threehalfs - ( x2 * y * y ));  // 2nd iteration, can be removed
    printf("Netown 迭代2次 = %f\n", y);
    return y;
}

//number为       = 5.000000
//转换为long     = 1084227584
//long的结果     = 1055349215
//转换为float    = 0.451858
//Netown 迭代1次 = 0.447141
//Netown 迭代2次 = 0.447214

//number = 5.000000, ret = 0.447214

可以发现代码计算的结果 0.447214 与真实结果 0.44721359 非常接近，小数点前五位都是一致的。

3. 步骤说明

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 快速反平方根
float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y = number;
    i = * ( long * ) &y;                     //step 1, evil floating point bit hack
    i = 0x5f3759df - ( i >> 1 );             //step 2, what the fuck?
    y = * ( float * ) &i;                    //step 3,
    y = y * ( threehalfs - ( x2 * y * y ));  //step4, 1st iteration
    y = y * ( threehalfs - ( x2 * y * y ));        // 2nd iteration, can be removed

    return y;
}

3.1. 第1步：讲number的地址转成long类型地址，并取long类型的值

1
2
3
4
5
6
7
8

i = * ( long * ) &y;
// 让i生成与y一样的内容，但是i是 long类型，y是float
// 不能使用强制类型转换，因为强制类型转换会丢失bit信息
// 此处目的是对float类型的number进行位运算，而float是不能进行位运行的，所以需要转换为long

// &y 获取到y的地址
// ( long * ) &y 然后将float的地址转换为 long的地址
// * ( long * ) &y 然后获取地址上的数值

3.2. 第2步：计算出反平方根的值（long类型下）

此处只有一句代码 i = 0x5f3759df - ( i >> 1 ) 但是这里非常复杂。这里得到的最终结果是 Ly=(3/2)*2^23*(127-μ) - 1/2*Lx (Lx是原来的i，Ly是计算结果，结果重新赋值给了i）。
这里μ为 0.04505 ，所以最终结果为 (3/2)*2^23*(127-μ) - 1/2*Lx 既 Ly = 0x5f3759df - (Lx >>1)

关于此处的解释，后面举例具体来说明。

F与L之间的转换关系为：log2(F)=(2^-23)*L + μ - 127

3.3. 第3步：重新回为浮点数

3.4. 第4步：使用牛顿迭代法提高精度

牛顿迭代是可以提高精度，前面得到了一个靠近的数值，但是由于μ的存在，是存在误差的，这里可以使用牛顿迭代法求到更具体的数值。

牛顿迭代法的公式是：

这里的f(x)是 $f(x) = \frac{1}{x^2}-a$，其导数函数是$f^{‘}(x)=\frac{-2}{x^{-3}}$，把函数和导函数代入牛顿迭代法公式：

1
2
3

y = y * ( threehalfs - ( x2 * y * y ));    // 1st iteration
// 代入值下
y = y * ( 1.5F- ( 0.5F * number * y * y ));   // 1st iteration

4. 举例来说：

number = 5.0F

float的二进制表示为

1
2
3
4
5
6
7
8
9

单精度的float，有32bit，
第1位位符号位，
第2~9位为指数，表示为E
最后23位为尾数，表示为M

1bit     8bit       23bit
符号位S  指数E       尾数M
0       10000001   01000000000000000000000  // 表示为float的时候，值为5.0F
0       10000001   01000000000000000000000  // 表示为long 的时候，值为1084227584

同样的一个32位的地址，可以解读成单精度的float，也可以解读成long类型的整型，下面是公式（F表示float类型的值，L表示long类型的值）：

根据上面两个公式，我们可以得到 float类型的值F，与 long类型的值L之间的关系如下(μ=0.04505）：

我们再把我们想要的内容答案 X = 1/sqrt(number) 代进去。（如下，Fy是我们想要的值）

两边取以2为底的对数，等式是成立的

获取到了上面的公式之后，可以利用 float类型的F与 long类型L的关系，把F换成L

至此，我们得到了代码中第2步的来由。

然后我们将 long 类型的Ly的结果，转成 float 类型，就能得到我们初步的答案。

验证一下：

现在，F = 0.5, L= 1084227584 的情况下，log2(F)=(2^-23)*L + μ - 127 是否成立

log2(F) = 2.3219280949

(2^-23)L + μ - 127 = (2^-23)L + 0.04505 - 127 = 2.29505

此处答案接近。

代入最终计算公式：

Ly=(3/2)2^23(127-μ) - 1/2*Lx

= (3/2)2^23(127-0.04505) - 1/2*1084227584

= 1055349171

1
2
3
4

1bit     8bit       23bit
符号位S  指数E       尾数M
0       10000001   01000000000000000000000
0       01111101   11001110101100110110011

将Ly转为Fy = 0.45185623

牛顿迭代一次：

1

y = y * ( threehalfs - ( x2 * y * y ))

y1 = y ( 1.5- ( 0.55 y y ))
= 0.45185623 ( 1.5- ( 0.55 0.45185623 0.45185623 ))
= 0.44714105083

一些在线二进制转换的工具：

浮点数表示：
https://tooltt.com/ieee/
https://tooltt.com/floatconverter/
进制转换：
https://www.sojson.com/hexconvert.html
LaTeX公式编辑器：
https://www.latexlive.com/

1. 首先需要安装lua

直接下载运行文件 http://joedf.ahkscript.org/LuaBuilds/ ，然后把lua.exe 加入到windows环境变量中。

2. 语法检测插件

• sublimelinter
• sublimelinter-lua
• sublimelinter-luacheck

3. 安装工具 luacheck

https://github.com/mpeterv/luacheck

直接下载运行文件exe就可以了，不需要全部下载 https://github.com/mpeterv/luacheck/releases/download/0.23.0/luacheck.exe

下载之后加入到windows环境变量中。

效果如下：

被黄色框框住的内容就是检查不通过的内容。

使用快捷键 ctrl + k, a 可以打开错误语法面板；

其它快捷键：

• ctrl + k, l 可以展示错误数量；
• ctrl + k, a 可以展示错误面板；
• ctrl + k, n 跳转到下个错误；
• ctrl + k, p 跳转道上个错误。

游戏里面的AI实现一般是状态机或者行为树。

状态机

状态机很好理解，就是AI会处于某一状态中，在不同条件下会进行切换，让AI处于正确的状态中。例如，一个怪物，有闲逛、战斗、逃跑三个状态。在没有遇到目标的时候，是处于【闲逛】状态，遇到了敌人，切换进入【战斗】状态；当血量低于5%或者远离出生点，进入【逃跑】状态。

行为树

行为树的执行就是从上到下，从左导游遍历整个树。每个节点执行之后都会返回true或者false，之后往上返回。不同节点遇到返回的结果执行方式不太一样。可能是往父节点返回，也可能是执行下一个子节点。具体结果要根据子节点的返回结果跟自身节点类型决定。
第一个节点是根节点，叶子是具体的操作行为，而中间节点是用来控制执行的顺序的。

组合节点

• Sequence 节点
  • AlwaysSequence 顺序执行
  • RandomSequence 每次执行都以随机序列去执行
• Select 节点
• IfElse 节点，有三个子节点，当第一个节点返回true，执行第二个子节点并返回子节点的值，否则执行第三个节点并返回节点的值。
• While 节点，有两个子节点，当第一个子节点返回true的时候，执行第二个子节点，然后重新开始执行流程；当第一个节点返回false的时候则执行完成，并且返回true。
• Root 节点，根节点，只有一个子节点。
• Probility 节点，随机执行节点

后缀

• 静态库
  • .a
  • .lib
• 动态库
  • .so
  • .dll

g++/gcc编译选项

• -o 指定输出目标的文件名
• -L 表示要链接的库所在目录
• -l 指定链接时需要的动态库，编译器查找动态库时有隐含的命名规则，即在给出的名字前面加上lib，后面加上.a或.so来确定库的名称。
• -shared 指定生成动态链接库
• -static 指定生成静态库
• -fPIC 表示编译为位置独立的代码，用于编译共享库
• -Wall 生成所有警告信息
• -ggdb 此选项将尽可能的生成gdb的可以使用的调试信息
• -g 编译器在编译的时候产生调试信息
• -c 只激活预处理、编译和汇编，也就是把程序做成目标文件，后缀为.o

静态库

静态链接：链接阶段，会将汇编生成的目标文件.o与引用到的库一起链接打包到可执行文件中。

• 静态库对函数库的链接是放在编译时期完成的；
• 程序在运行时与函数库再无瓜葛，移植方便；
• 浪费空间和资源，因为所有相关的目标文件与牵扯到的函数库被链接合成一个可执行文件。

linux下静态库命名规范必须是lib[name].a，lib是前缀，是必须的，扩展名为.a。

创建静态库

• 首先将代码编译成目标文件.o
  • g++ -c Test.cpp
• 通过ar工具将目标文件打包成.a静态文件
  • ar -crv libtest.a Test.o

动态库

动态库在程序编译时并不会被链接到目标代码中，而是程序运行时才被载入。不同的应用程序如果调用相同的库，那么在内存里只需要有一份被该共享库的实例，避免了内存上的浪费。

• 动态库把一些库函数的链接载入推迟到程序运行的时期；
• 抗原实现进程之间的资源共享；
• 将一些程序升级变得简单；
• 甚至可以真正做到链接载入完全由程序员在代码中控制。

调试帮助

nm 命令

nm命令可以打印出库中的涉及到的所有符合。

• 在库中被调用，但是没有在库中定义的，用U表示
• 在库中定义的函数，用T表示
• 弱态符合，用W表示，虽然在库中被定义，但是可能被其他库中的同名符合覆盖。

1

nm libtest.h

ldd 命令

ldd命令可以查看一个可执行程序依赖的共享库。

1

ldd libtest.so